uncertainty and individuality
Consider one particle that has an uncertainty in its position. Here, a Gaussian distribution represents this uncertainty about 1-dimension (x). The peak represents the most likely place to find this particle, with ever-diminishing likelihood as x→-∞ or x→+∞.

Now consider two particles of identical nature. By ‘identical’, I mean that any differences between the particles are completely undetectable to the observer. Thus, excepting position, these particles are identical to the observer.
If these particles also have uncertainties in their positions, their uncertainties will overlap.
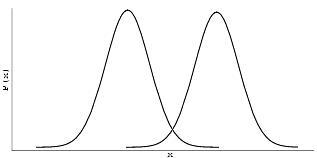
As the particles have overlapping uncertainties in their position, to the observer, there are not two discrete particles. Unless the observer can measure the position of both particles simultaneously, one particle can partially serve as the other.
The degree to which both particles behave as a single entity (rather than two discrete entities) would be proportional to the inability to know the position of both particles simultaneously.

Now consider two particles of identical nature. By ‘identical’, I mean that any differences between the particles are completely undetectable to the observer. Thus, excepting position, these particles are identical to the observer.
If these particles also have uncertainties in their positions, their uncertainties will overlap.

As the particles have overlapping uncertainties in their position, to the observer, there are not two discrete particles. Unless the observer can measure the position of both particles simultaneously, one particle can partially serve as the other.
The degree to which both particles behave as a single entity (rather than two discrete entities) would be proportional to the inability to know the position of both particles simultaneously.


1 Comments:
Quantum mechanically, it doesn't even matter how much the uncertainties overlap, or whether they do at all. Any 2 electrons, anywhere in the universe, can be swapped with no observable effect. So you don't have one wavefunction for this electron, and another for that; it's just one wavefunction for all the electrons everywhere.
The swap does affect the (unobservable) phase of the wavefunction, and that effect is different for fermions and bosons. That's why fermions (but not bosons) have Fermi degeneracy pressure (which stops small burnt-out stars from collapsing into black holes) and bosons (but not fermions) form Bose-Einstein condensates.
Post a Comment
<< Home